Concurrent Atomistic Continuum (CAC) Method
The concurrent atomistic-continuum (CAC) method is a partitioned-domain multiscale modeling technique that is applicable to nano/micro-scale thermo/mechanical problems in a wide range of monatomic and polyatomic crystalline materials. A CAC simulation model, in general, partitions the simulation cell into two domains: a coarse-grained domain and an atomistic domain. Distinct from most concurrent multiscale methods in the literature, CAC employs a unified atomistic-continuum integral formulation with elements that have discontinuities between them; also, the underlying interatomic potential is the only constitutive relation in the system. As such, CAC admits propagation of displacement discontinuities (dislocations and associated intrinsic stacking faults) through a lattice in both atomistic and coarse-grained domains, as shown in the figure below.
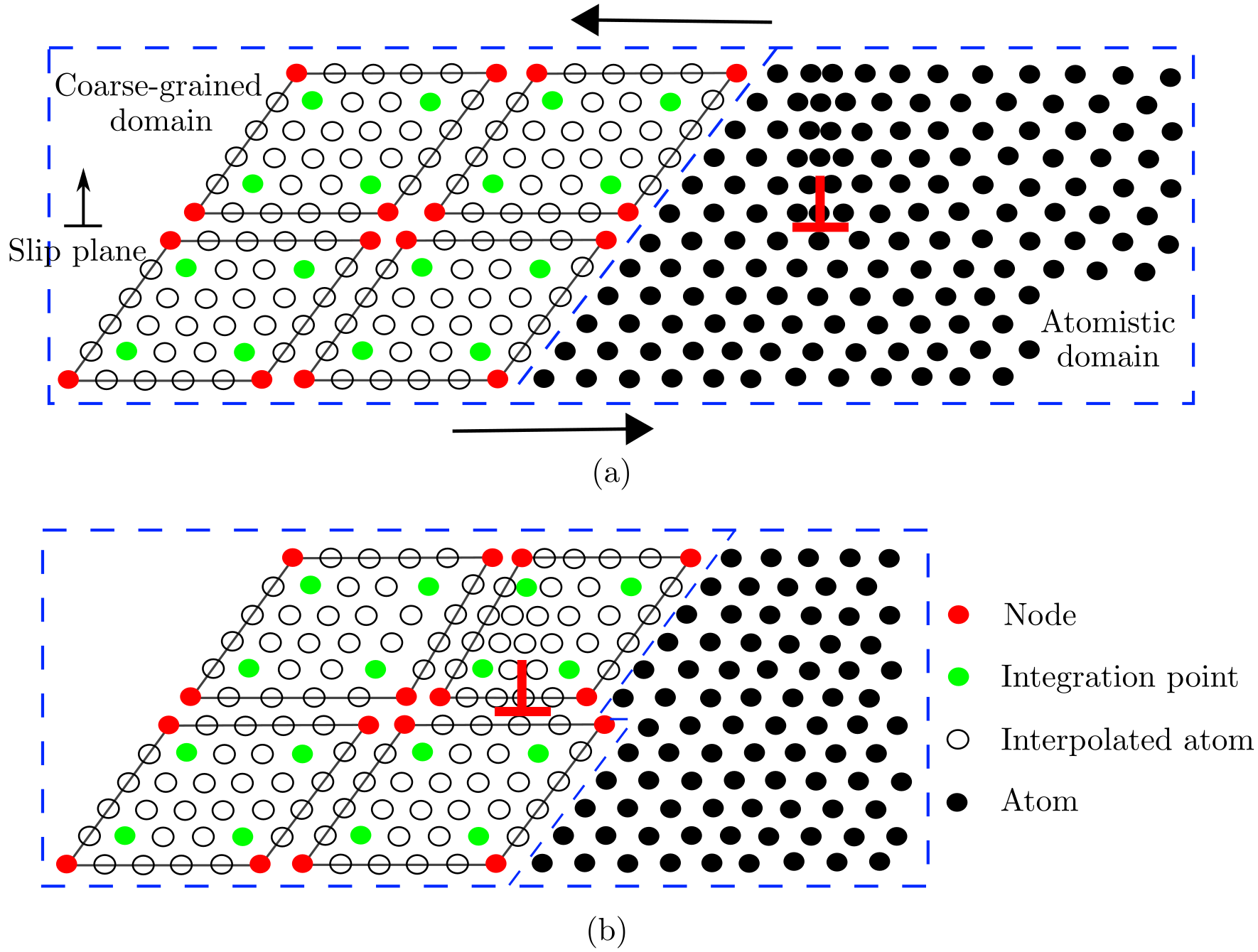
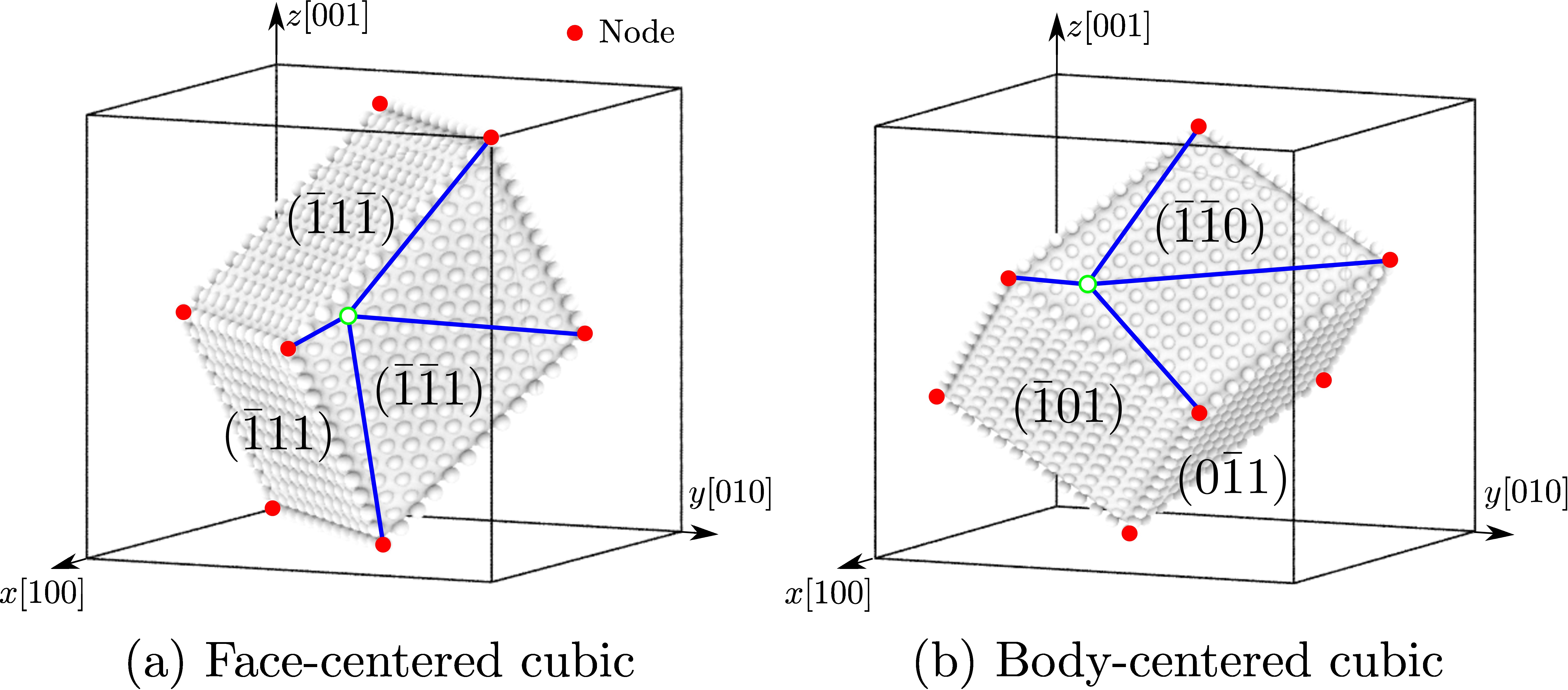
In a (big) nutshell, CAC
- describes certain lattice defects and their interactions using fully resolved atomistics;
- preserves the net Burgers vector and associated long range stress fields of curved, mixed character dislocations in a sufficiently large continuum domain in a fully 3D model;
- employs the same governing equations and interatomic potentials in both domains to avoid the usage of phenomenological parameters, essential remeshing operations and ad hoc procedures for passing dislocation segments between the atomistic and coarse-grained domains.